Proposto da Zenone di Elea (filosofo greco vissuto nel V secolo a.C.), il paradosso di Achille e la tartaruga è uno dei più famosi paradossi ereditati dalla filosofia classica. Una delle descrizioni più celebri del problema è quella dello scrittore argentino Borges, il quale scrive:
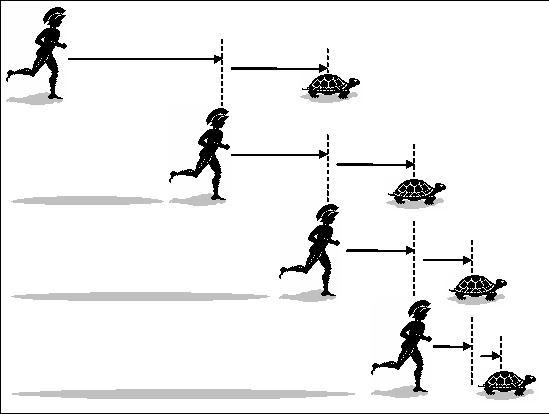
“Achille, simbolo di rapidità, deve raggiungere la tartaruga, simbolo di lentezza. Achille corre dieci volte più svelto della tartaruga e le concede dieci metri di vantaggio. Achille corre quei dieci metri e la tartaruga percorre un metro; Achille percorre quel metro, la tartaruga percorre un decimetro; Achille percorre quel decimetro, la tartaruga percorre un centimetro; Achille percorre quel centimetro, la tartaruga percorre un millimetro; Achille percorre quel millimetro, la tartaruga percorre un decimo di millimetro, e così via all’infinito; di modo che Achille può correre per sempre senza raggiungerla.”
Il paradosso è stato proposto da Zenone per sostenere la tesi del suo maestro Parmenide secondo cui il movimento sia soltanto un’illusione.
Già nell’antica Grecia, alcuni filosofi presentarono ovvie confutazioni a tale paradosso, dimostrando praticamente la sua inesattezza, ad esempio camminando. Eppure rileggendo il testo del problema ci resta la convinzione che in qualche modo Zenone abbia ragione. E’ in questa direzione, del tutto filosofica, che ha avuto grande successo il paradosso di Achille e la tartaruga: ovvero provare a vedere e interpretare la realtà con idee e concezioni diverse da quella usuale e radicata in noi, una visione che ad esempio non ci porta ad interpretare il paradosso come palesemente irreale.
Da un punto di vista strettamente matematico, invece, il problema è stato risolto completamente dal concetto di “serie geometrica”, ovvero quando si è realizzato che una somma infinita di addendi può portare anche ad un risultato finito.
Nel nostro caso, infatti, con semplici applicazioni di formule sul moto rettilineo uniforme possiamo sommare i tempi in cui Achille percorre ciascun segmento e vedere che la serie (cioè la somma infinita) di questi tempi converge ad un numero finito, che sarebbe il momento in cui effettivamente Achille raggiunge la tartaruga.
Alessandro La Farciola
