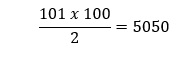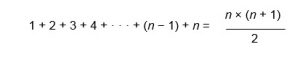Qual è il risultato della somma dei numeri da 1 a 100? E’ questa la domanda che secondo la leggenda fece il maestro di Carl Friedrich Gauss a Gauss stesso quando aveva 8 anni, pensando di tenerlo impegnato per un po’. La risposta, d’altronde, fu immediata da parte del bambino: 5050. Come ha fatto? E’ davvero così immediato? Sì, se si conosce il trucco giusto. Proviamo a sommare:
1+2=3, 3+3=6, 6+4=10, …
Si potrebbe continuare in questo modo, ma sarebbe lungo e noioso.
Come si può ragionare allora? A noi interessa:
1+2+3+4+5+···+97+98+99+100
Riscriviamo ora la stessa riga ma al contrario e sommiamo in verticale: cosa otteniamo?
| 1 + 2 | + 3 +···+ | 98 + | 99 + 100 | |||||
| 100 +99 + 98 +···+ | 3 | + | 2 + 1 | |||||
| 101+101+101 +···+ 101 | + 101 + 101 | |||||||
| | | {z | } | ||||||
Si è quindi ottenuto che la somma delle due righe è pari a 101 × 100, ma dato che noi vogliamo solo una riga e non la somma di entrambe basta dividere per 2. Il totale insomma è:
Lo stesso ragionamento si può generalizzare e la formula appena utilizzata per calcolare la somma dei primi 100 numeri funziona per qualsiasi cifra al posto di 100. Ovvero, per ogni numero n:
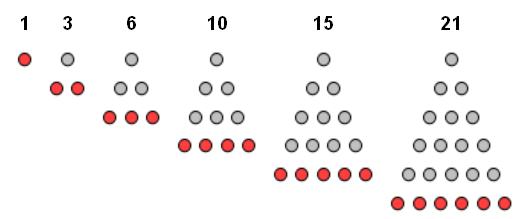
Carl Friedrich Gauss è stato un grandissimo matematico vissuto a cavallo tra il ’700 e l ’800, ma tale relazione esistente tra i numeri incuriosì anche gli antichi Greci, in particolare i pitagorici, che ne scoprirono gli effetti costruendo i cosiddetti numeri triangolari (vedi Immagine).
Ognuno di questi numeri, infatti, si ottiene sommando a partire da 1:
- 1
- 1+2=3
- 1+2+3=6
- 1+2+3+4=10
- 1+2+3+4+5=15
- 1+2+3+4+5+6=21
Ma allora come si calcola l’n numero triangolare?
Semplice, con la formula di Gauss!
Alessandro La Farciola
